Modelo hidrodinámico multicapas (PIMAS-HYDRO)
Este es un modelo numérico que resuelve las ecuaciones de aguas someras (shallow-water equations), mediante un esquema euleriano-lagrangiano. La parte advectiva de las ecuaciones de movimiento se resuelve aplicando el método de las características, a través de una interpolación explicita de segundo orden. La parte difusiva es resuelta con una formulación de tipo ADAMS-BASHFORTH en diferencias finitas centradas. La turbulencia se resuelve a través de modelos de orden cero (longitud de mezclado) y de primer orden (κ-ε). Es un modelo multicapas, en el cual la discretización de las ecuaciones se realiza utilizando mallas tipo Staggered-Cell, con espaciamiento de celdas rectangulares no uniforme. El modelo puede ser aplicado en dominios irregulares, para llevar a cabo simulaciones en cuerpos de agua continentales (ríos, lagos, embales, etc.), costeros (lagunas, estuarios, humedales) y marinos (zona costera y costa afuera).

Simulación de la hidrodinámica de un sistema río-laguna-mar
Modelo hidrodinámico y de transporte de contaminantes ANAITÉ/2D
Para la parte hidrodinámica, este modelo resuelve las ecuaciones de flujo variable del agua en lámina libre o ecuaciones bidimensionales de Saint Venant. Dichas ecuaciones describen el flujo bidimensional no estacionario promediado verticalmente, representan los principios de conservación de la masa y de la cantidad de movimiento y son obtenidas a partir de las ecuaciones de Navier-Stokes-Reynolds (N-S-R). También se utiliza el método euleriano-lagrangiano resuelto en una aproximación de segundo orden para la solución de las ecuaciones y malla tipo Staggered-Cell, en la cual se evalúan los escalares en el centro de la celda y las magnitudes vectoriales en las caras. Para evaluar la difusión, el modelo permite la selección entre varios modelos de turbulencia, dentro de los cuales se encuentra el propuesto por Mellor-Yamada. El módulo de transporte de contaminantes resuelve la ecuación de Advección-Difusión-Reacción para 22 diferentes parámetros de calidad del agua, incluyendo fisicoquímicos, metales pesados y HAPs. Además incluye un módulo donde se resuelve un índice de calidad del agua en el cual se integran todos los parámetros resueltos por el modelo, y que ha sido especialmente diseñado para ecosistemas acuáticos afectados por actividades industriales.
Modelo de oleaje costero
El modelo numérico de oleaje resuelve la ecuación de Berhkoff, conocida como la ecuación de pendiente suave en su forma elíptica, para profundidades indefinidas y análogamente para zonas someras, considerando la celeridad de grupo de ola en función de la profundidad y de la aceleración de la gravedad. La ecuación se ha subdividido en tres ecuaciones para calcular, de forma simultánea, la dirección, altura de ola y fase de la ola. La solución del sistema de ecuaciones se lleva a cabo por un algoritmo de relajación para el cálculo de la fase de la ola. Se emplea un esquema de volumen finito con aproximación elíptica y un mallado tipo Staggered-Cell, con la opción de tener un refinado de malla en zonas donde se encuentren obras de protección o estructuras que modifiquen el oleaje para su estudio. El modelo ha sido calibrado y perfectamente validado, mediante la comparación con soluciones analíticas que presentan ejemplos de aplicación en condiciones simples. De igual forma, el modelo ha sido aplicado para el estudio de parámetros de oleaje, variación de la superficie libre, y fenómenos que modifican el oleaje (reflexión, refracción, difracción y rompiente), en diversas regiones costeras del país.

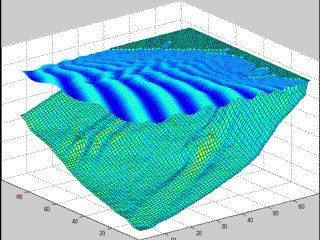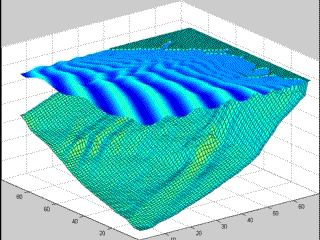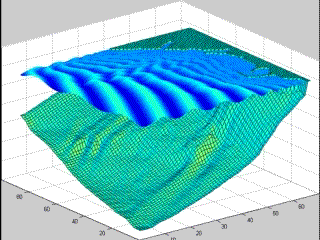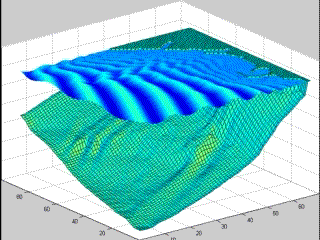
Simulación de oleaje costero en obras de contención
Módulo de transporte de sedimentos
Este módulo está integrado a los modelos hidrodinámicos. Además, también toma en cuenta la propagación del oleaje y sus fenómenos asociados (difracción, reflexión y rompiente principalmente) en la superficie libre, que permiten el transporte de partículas de forma independiente en cualquier dirección en el espacio, provocado por el campo de velocidades y la dispersión turbulenta (movimiento aleatorio de tipo Browniano). Los mecanismos de dispersión y resuspensión de partículas que se emplean son representados a través de modelos estocásticos, los cuales describen el movimiento por medio de una función de probabilidad. El desarrollo del módulo permite incorporar el cálculo de una parte lagrangiana de las ecuaciones de movimiento (advección) con una parte euleriana (difusión molecular y turbulenta) del fluido, para determinar, en conjunto con la ecuación de transporte, el movimiento de los sedimentos en un esquema continuo dentro del flujo. Es decir, el movimiento de un escalar con una concentración inicial y una final la cual involucra los procesos de suspensión, sedimentación y resuspensión en columna de agua. La frontera para la sedimentación se ubica sobre la subcapa laminar (muy cerca del fondo), en esta zona se decide probabilísticamente, cuáles son las partículas que se resuspenden y cuáles son las que se sedimentan.

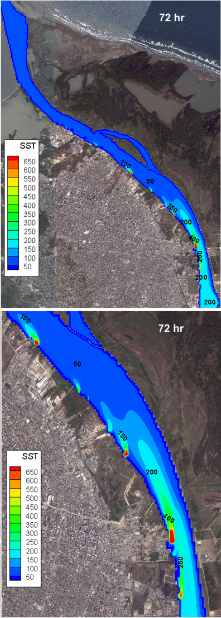
Imagen de satélite y simulación de la pluma de sedimentos de un río en la zona de la desembocadura
Módulo lagrangiano de partículas
El módulo para el transporte de partículas está dado bajo un enfoque lagrangiano; las partículas son sembradas o colocadas siguiendo una ley exponencial de concentraciones o mediante una posición inicial en el espacio tridimensional. Para el movimiento de partículas se considera el peso específico de cada partícula, así como de la velocidad de caída de esta. El movimiento de las partículas es dependiente del fluido, y los mecanismos de dispersión y resuspensión tienen un carácter aleatorio, cuyo comportamiento puede ser representado por el empleo de modelos estocásticos, los cuales describen el movimiento de las partículas sólidas por medio de una función de probabilidad. El proceso físico corresponde al seguimiento de muchas partículas, empleando un campo hidrodinámico y un campo de viscosidades turbulentas, que representaría la intensidad de la turbulencia sobre todo el dominio de la simulación. Esto permite obtener la ubicación o existencia de una partícula en un cierto punto. La validación del módulo se llevó a cabo con dos casos con solución numérica conocida, empleando una transformación discreta-continua con el método PIC (Partícula en Celda), obteniendo errores relativos promedio porcentuales menores al 10% en ambos casos. Asimismo, el módulo ha sido aplicado, tanto para casos teóricos, como para casos reales.
